2020年4月より当社開発グループにエンジニアとして入社した安部と申します。今回のDevelopers Blogではアルゴリズムについて初心者ながら自分への復習も兼ねてお話しさせていただきます。
目次
題材を選んだ理由
アルゴリズムについての研修で、今までがっつりアルゴリズムに触れる機会がなかったので、改めてしっかり勉強してみたいなと思ったのがきっかけです。
研修を通して感じたこと
アルゴリズム の研修課題に取り組んでいる際に、回答例をみて「こんな発想ポンと出てこねぇ…」と感じることが多々ありました。もちろん基礎的なアルゴリズムの知識も重要ですが、そのアルゴリズムを実際に直面している問題にどのように取り入れるのか、といった経験は非常に重要だなと思いました。簡単な発想の転換で難解に見えた問題でも効率的なコードで実現することができます。やはり取り組んだ問題の経験は大事だなと感じました。
問題
せっかくなので、発想の転換系で10ANTZ (ants : アリ)に因んだ問題を一つ紹介したいと思います。
Ants (POJ No. 1852)
n匹のアリが長さLcmの棒の上を毎秒1cmの速度で歩いています。アリは棒の端まで歩くと棒の下に落ちていきます。二匹のアリが出会うと、それぞれ反対を向いて歩いていきます。各アリiについて、現在の棒の左端からの距離xiはわかりますが、どちらの方向を向いているのかはわかりません。全てのアリが棒から落ちるまでにかかる最小の時間と最大の時間をそれぞれ求めなさい。
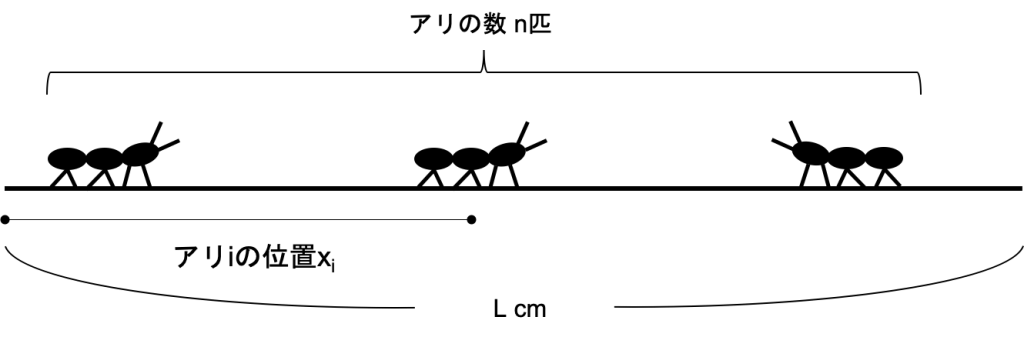
いかがでしょうか。アリ同士が出会った場合とか各アリがどちらの方向を向いているかわからない、など結構考えなければならない部分が多いかと思います。このような問題を解く場合にどのようなアルゴリズムでどうやって効率をあげていけばいいかといった部分を解説していきたいと思います。10匹のアリで、と言いたいところですが、少し複雑になってしまうので簡単化のためにアリの数は3匹(n=3)、竿の長さは10cm(L=10)でやっていきたいと思います。
単純な解き方
アリが落ちるまでの最小の時間と最大の時間を求める際に、まず各アリの向きがどのパターンのときに最小、最大となるのかを考えなければなりません。しかし、どのパターンが最小、最大となるのかわからないので、一つずつ試していくしかなさそうです。そのうえ、アリの総数もわからないので、for文のネストで全パターン試すといったやり方も難しそうです。
そこで、まずは再帰を利用した全探索を試してみたいと思います。
コードが以下になります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
<?php // アリが全て落ちるまでの時間を計算する function calc($l, $n, $ants) { $fallAnts = array_fill(0, $n, 0); $time = 0; // 全てのアリが落ちるまで行う while (true) { // 各アリを向いている方向に進ませる for ($i = 0; $i < $n; $i++) { // 既に落ちているアリはスルー if ($ants[$i]['position'] == 0 or $ants[$i]['position'] == $l) { $fallAnts[$i] = 1; // 落ちたアリカウンター continue; } // アリを1cm進める(左向き:-1なら-1、右向き:1なら+1) $ants[$i]['position'] += $ants[$i]['direction']; // アリ同士の衝突判定 for ($j = 0; $j < $n; $j++) { // ぶつかっていたらお互いに反転 if ($i != $j and $ants[$i]['position'] == $ants[$j]['position']) { $ants[$i]['direction'] *= -1; $ants[$j]['direction'] *= -1; } } } // 全てのアリが落ちたらreturn if (array_sum($fallAnts) == $n) { return $time; } $time += 1; } } // アリの向きを全パターン試す function solve($i, &$min, &$max, $ants, $l, $n) { // ベースケース if ($i < 0) { return false; } $min = min($min, calc($l, $n, $ants)); $max = max($max, calc($l, $n, $ants)); // ants[i-1]を右に向ける場合 $ants[$i - 1]['direction'] = 1; solve($i - 1, $min, $max, $ants, $l, $n); // ants[i-1]を左に向ける場合 $ants[$i - 1]['direction'] = -1; solve($i - 1, $min, $max, $ants, $l, $n); } function init() { $l = 10; $n = 3; $xList = [2, 5, 7]; $min = INF; $max = 0; // アリの位置と向きを初期化(direction= -1:左, 1:右) $ants = array(); for ($i = 0; $i < $n; $i++) { $ants[] = ['position' => $xList[$i], 'direction' => 1]; } solve($n, $min, $max, $ants, $l, $n); echo 'min = ' . $min . 'max = ' . $max; //echo calc($l, $n, $ants); } init(); |
どちらかというとアリが落ちるまでの時間を計算している部分の方が複雑になっていますが、重要なのはアリの向きのパターンを探索しているところです。上のコードで実際に全探索している箇所は以下の部分です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
function solve($i, &$min, &$max, $ants, $l, $n) { // ベースケース if ($i < 0) { return false; } $min = min($min, calc($l, $n, $ants)); $max = max($max, calc($l, $n, $ants)); // ants[i-1]を右に向ける場合 $ants[$i - 1]['direction'] = 1; solve($i - 1, $min, $max, $ants, $l, $n); // ants[i-1]を左に向ける場合 $ants[$i - 1]['direction'] = -1; solve($i - 1, $min, $max, $ants, $l, $n); } |
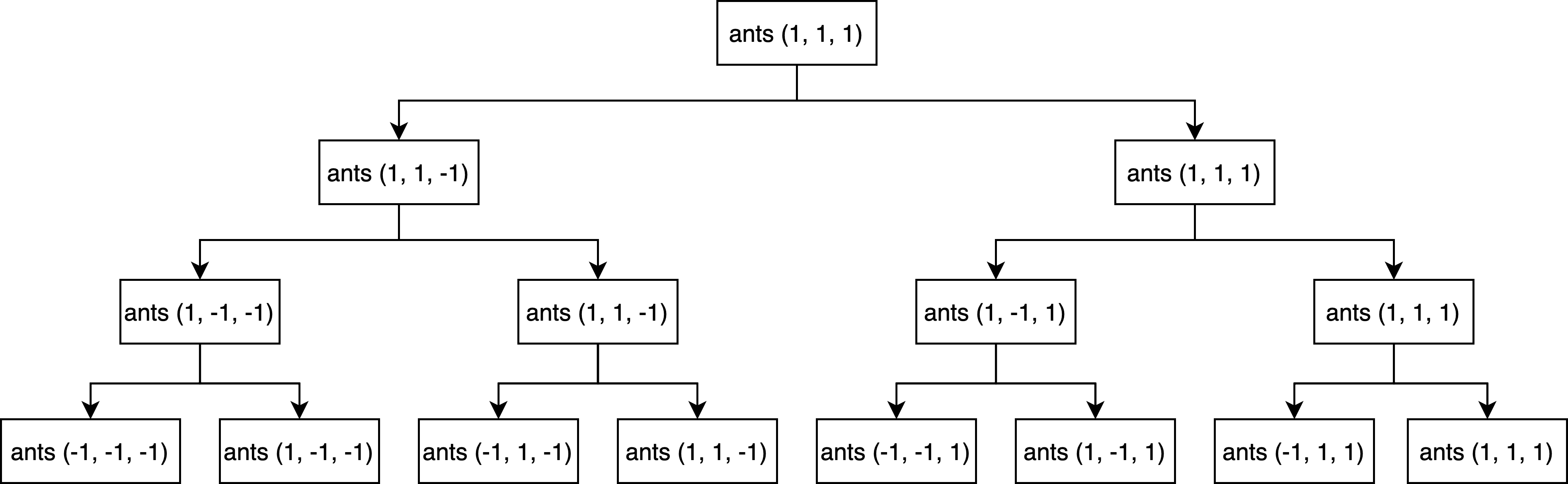
上のコードの動きを簡単に図にすると以下のようになります。(アリの向きが左なら-1、右なら1と置いている)
順番にアリをフォーカスしています。ある1匹のアリを見たときに、そのアリが左を向いている場合と右を向いている場合で全てのアリが落ちるまでの時間を計算しています。各アリに対して右向きと左向きの2パターンを試しているので計算量はO(2n+1)ほどになります。
図を見てみるとants(1, 1, 1)やants(1, 1, -1)など、無駄に同じ処理をしている部分があり効率が悪いです。こう言った無駄を省くために既に調べたアリの向きのパターンを記録しておけば、同じパターンが来た場合にそこから結果を取り出すことができるので効率が良さそうです。
動的計画法
そこで、再帰処理の無駄を省くために動的計画法のメモ化を利用します。
メモ化とは同じ変数で計算処理を行おうとした場合に事前に記録しておいた結果を返すようにすることで同じ計算をしないようにすると言ったものです。
今回の問題をメモ化すると以下のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
function solve($i, &$min, &$max, $ants, $l, $n, &$antsMemo) { // ベースケース if ($i < 0) { return false; } $directions = implode(array_column($ants, 'direction')); // 向きのパターンを記録 if (!in_array($directions, $antsMemo)) { $min = min($min, calc($l, $n, $ants)); $max = max($max, calc($l, $n, $ants)); $antsMemo[] = $directions; } // ants[i-1]を右に向ける場合 $ants[$i - 1]['direction'] = 1; solve($i - 1, $min, $max, $ants, $l, $n, $antsMemo); // ants[i-1]を左に向ける場合 $ants[$i - 1]['direction'] = -1; solve($i - 1, $min, $max, $ants, $l, $n, $antsMemo); } |
それぞれのアリの向きを記録するためのリストを用意してあげ、計算の処理の前にリストの中身を確認する処理を追加しました。非常に単純ですが、これだけで計算量はO(2n)になります。本当に簡単な処理を追加してあげただけですが、この「全探索をメモ化」して効率をあげる手法は競技プログラミングの世界でもよく使われる手法だそうです。そう言われるとなんか凄そうですね。笑
発想の転換
しかし、今回の問題に関して、上記のような手順を踏まずともより簡単に解く手段が存在します。まず最小の時間について考えてみます。最小の時間は全てのアリが近い方の端に向かえばそれが最小になります。この場合、アリ同士が出会うことはないことがわかります。
次に最大の場合ですが、これはアリ同士が出会った場合の考えを変えれば非常に簡単なものになります。この問題ではアリを個別に認識する必要がないところがミソです。
実は、アリ同士が出会ったとしてもそのまますれ違って進んだと考えてしまって問題ないのです。図にして考えてみます。

まず、アリ同士を区別していた場合は出会った際にきちんと逆向きに進ませてあげなければいけません。ですが、問題の内容的にはアリを区別する必要はないのです。

区別しなければ逆向きに進んだ場合とすれ違って進んだ場合で動きは変わらないことがわかります。
そうすると、全てのアリは他のアリに邪魔されることなく動いていることになるので、端までの距離が最大になるパターンが最大の時間になります。
このように考えると、最小の時間も最大の時間も全てのアリを一回ずつ調べればいいので、ものすごく効率よく解くことができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
function solve2($n, $l, $ants) { // 最小の時間を計算 $min = 0; // 各アリが落ちるまでの時間が最小になるパターンのうち、一番最後に落ちるアリの時間を求める for ($i = 0; $i < $n; $i++) { $min = max($min, min($ants[$i]['position'], $l - $ants[$i]['position'])); } // 最大の時間を求める $max = 0; // 各アリが落ちるまでの時間が最大になるパターンのうち、一番最後に落ちるアリの時間を求める for ($i = 0; $i < $n; $i++) { $max = max($max, max($ants[$i]['position'], $l - $ants[$i]['position'])); } echo 'min = ' . $min . ' max = ' . $max; } |
実際に上記のコードで先ほどまでのものと同じ結果が得られます。さらにこちらはfor文をアリの数だけしか回していないので計算量もO(n)となり速度も圧倒的です。個人的にこの問題、一般的な手順でもそれなりの速度で解くアルゴリズムが作れるが、問題文から本質を理解して解答を導けば、単純で効率のよいものが得られる、といった点がとてもきれいな問題だと思います。
まとめ
さて、今回のDevelopers Blogでは問題に対してどのようにアルゴリズムを選択するのか、そのアルゴリズムを効率よくするための手法について例題をもとに簡単ですが紹介させていただきました。しかし、アリ同士がすれ違うことができる点に気付けるかどうかはアルゴリズムの知識よりも柔軟に物事を考える努力が必要だと感じました。
弊社エンジニアの先輩方は物凄い知識と経験をもっている方々ばかりなので、先輩方のために少しでも早く役立てるよう、勉強と合わせて頭の柔らかさも鍛えていきたいと思います。
参考文献
秋葉拓也, 岩田陽一, 北川宣稔 (2012/03/20) 問題解決のアルゴリズム活用力とコーディングテクニックを鍛える プログラミングコンテストチャレンジブック 第2版 マイナビ出版