はじめに

19新卒Unityエンジニアの大川です。

弊社エンジニアのスキルアップを図るプロジェクトが始まるとのことで、

試験的に「巡回セールスマン問題を焼きなまし法を使用して解決する」という課題が私に与えられました。

そのアウトプットとして今回の記事を書いていきます。

上記の課題を解決する方法が、日本語の情報でよくまとめられていなかったので、

同じ問題を解決したい方にとっても参考になる記事を書いていきたいと思います。

問題を解決にあたって、普段使い慣れているC#を用い、

結果を視覚的に確認できるようにするため、Unityを使用していきます。

巡回セールスマン問題とは

もし、あなたが日本全国を巡るセールスマンだとします。

ある日上司から、47都道府県の県庁所在地に営業をかけて来いと命じられました。

あなたは特殊能力の持ち主なので、県庁所在地間を直線で移動できます。

この時、どの順番で県庁所在地を訪問するのが効率が良いでしょうか？

条件としては、どこから営業を開始してもよく、最後に開始地点まで戻る必要があります。

解を求める上での問題点

総移動距離がもっとも短い経路を求めるためには、

すべての組み合わせの総距離を求めて、一番短いものを調べる必要があります。

すべての組み合わせの数は、訪問地点をNとすると

点のつなぎ方としてはN!通り

その中で時計回り・半時計周りで経路は同じなので１/２

さらに一つの経路はどこから開始しても同じなので１/N

まとめると

N!/2N=(N-1)!/2

になります。

47都道府県の場合組み合わせを電卓で計算したところ…

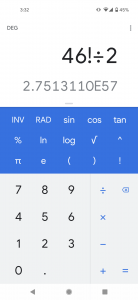
2.7513110E57

Eは10の何乗かなので、何通りでしょう…

27,513,110*10^50

=2751311000000000000000000000000000000000000000000000000000

=二十七阿僧千祇百五十一三一千恒百河十沙一極

普段使うことのない単位しか出て来ないですね…

現在のコンピュータでは、何億年かけても計算が終わらない組み合わせです。

結論から言いますと、最短経路を求めるのは不可能です。

しかし、次から説明する方法を使用することで、最短に近い結果を得ることができます。

貪欲法

方法

開始地点から一番近い距離を順番につないでいく方法です。

この時、開始地点から距離を調べる地点は46個

２つ目の地点からは45個

３つ目の地点からは44個となるので、

46+45+44+…+2

=1080回

距離を計算するだけで済みます。

デメリット

この方法だと、結果がこちらになります。

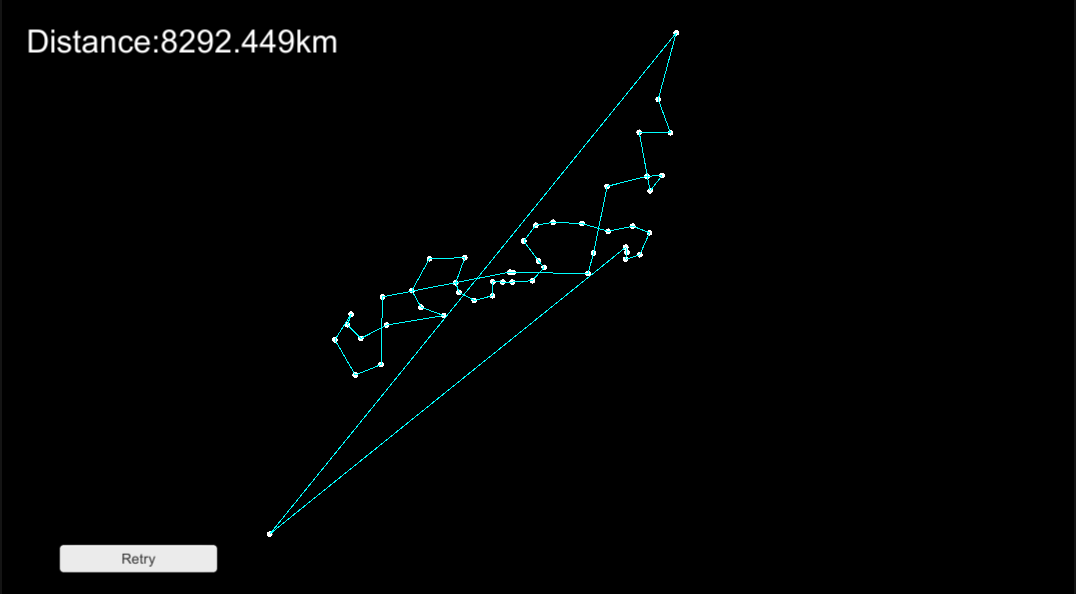
近い順につないでいくので、長いものが最後につながれるので最適な経路とは言えないですね。

焼きなまし法

今回の問題の例で例えますと、

サラリーマンが自分の足で体力がなくなるまで日本一周して、

その中でどの経路が一番良かったか結論を出します。

日本一周するたびにサラリーマンの体力は減っていきます。

（サラリーマンの体力は超人レベルです）

体力が多いうちは、距離が遠い次の県庁所在地にも気まぐれで向かいますが、

体力がなくなるとほとんど確率で近い次の県庁所在地にしか行かなくなります。

このようにしてランダム性を持たせることで、最適な経路を探していきます。

今回は体力で例えましたが、本来焼きなまし法は、温度で例えられます。

貪欲法×焼きなまし法

この二つを組み合わせることによって、最適な経路を求めることができます。

貪欲法で近い県庁所在地を調べて行くとき、

途中で前回調べた距離よりも長い県庁所在地があった場合、

サラリーマンの体力に応じた確率で長い県庁所在地を選択するようにします。

そうすることによって、毎回異なった経路になり、

サラリーマンの体力がなくなるまで、日本一周の経路を求め続けることによって、

最短距離に近い経路を求めることができます。

貪欲法の近い距離しか選択しない問題に、焼きなまし法を取り入れることによって、

近い距離しか選択しなかった場合の経路から、

極端に長い距離を選択する場合の経路までをカバーすることが可能になりました。

また、サラリーマンの体力の減少をゆっくりすることによって、

より高い精度の結果を得ることができます。

体力の減少をゆっくりにすると、ループ回数が増え、計算時間がかかってしまうので、

経路の数に応じてこちらの度合いを調整する必要があります。

処理の流れ

アルゴリズムを図示化すると以下になります。

実行結果

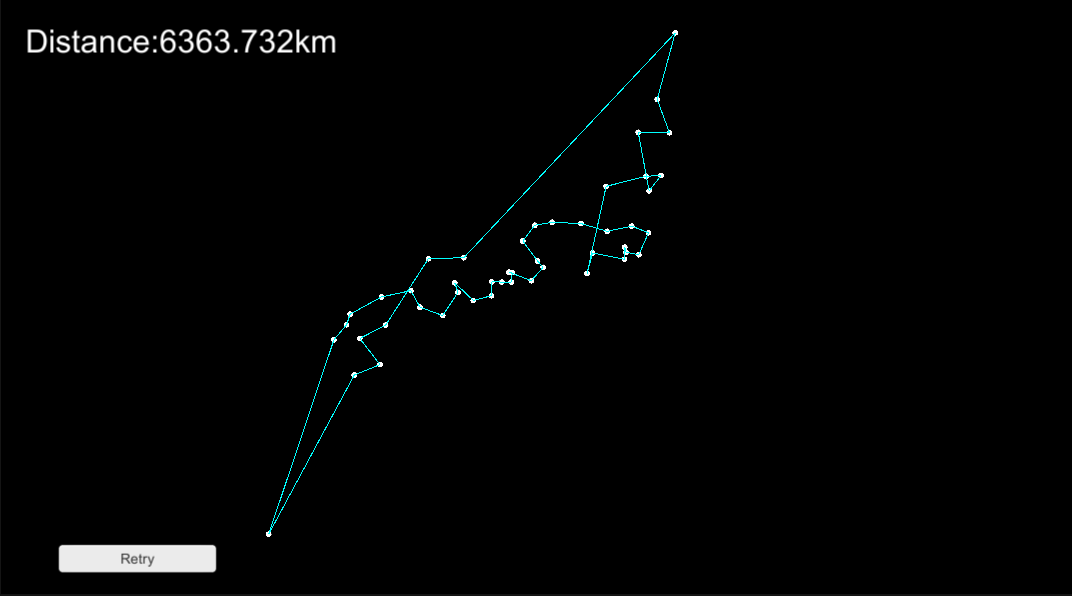
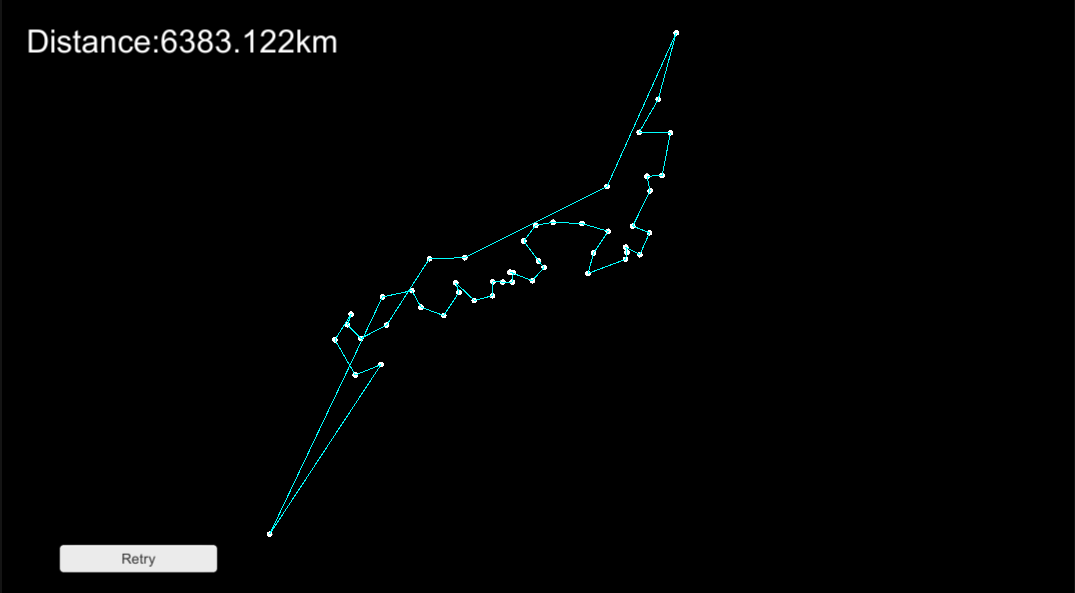
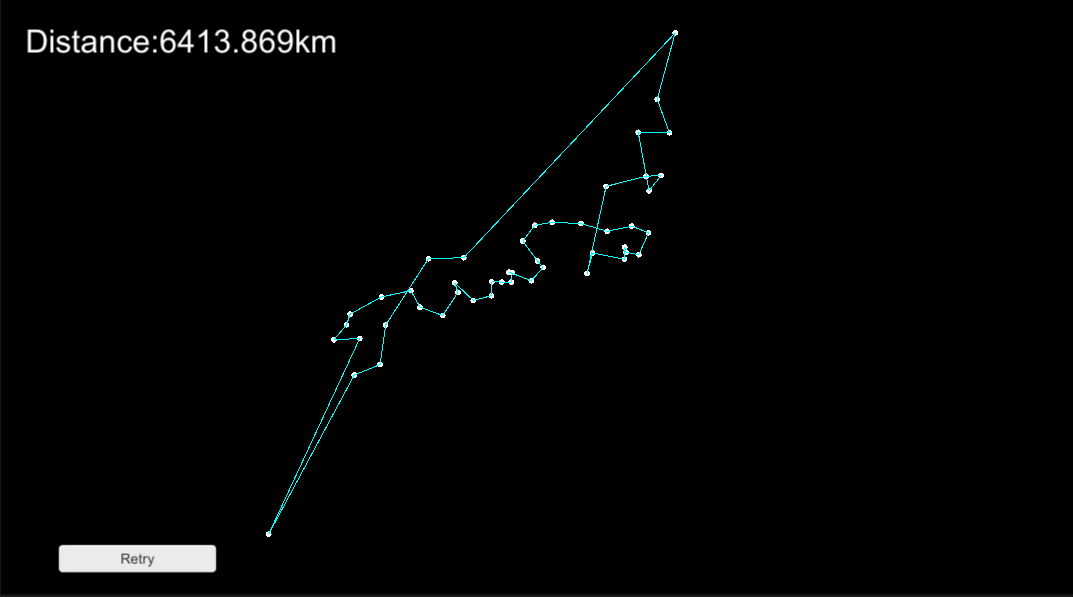
毎回得られる結果は異なりますが、貪欲法だけの時よりも見たところ、適切な答えが得られているように見えます。

他の方法

今回は貪欲法と焼きなまし法を組み合わせて問題を解決しましたが、

貪欲法以外も組み合わせられる方法があります。

まず、ランダムに県庁所在地をつないで適当な経路を作成します。

適当に２つの地点を選択して経路を入れ替えます。

総距離を計算して短くなれば入れ替えた経路を採用しますが、

距離が長くなった場合焼きなまし法で採用するしないを判定します。

２つの地点を入れ替えるたびに、サラリーマンの体力を減らしていき、

体力がなくなるまで入れ替えを続けます。

その結果、最終的に最適に近い経路を得ることができます。

ソースコード

プロジェクト全体はこちらになります。

https://github.com/k-okawa/TspByUnity

Unityのバージョンは2019.4.8f1です。

こちらには主要なコードを抜粋して掲載します。

public class PrefectureData
{
    public readonly int id;
    // 県庁所在地名
    public readonly string name;
    // 経度
    public readonly double longitude;
    // 緯度
    public readonly double latitude;

    // Unity上のオブジェクト
    public GameObject ownObj;

    public PrefectureData(List<string> csvLine)
    {
        id = int.Parse(csvLine[0]);
        name = csvLine[1];
        latitude = double.Parse(csvLine[2]);
        longitude = double.Parse(csvLine[3]);
    }
}

public class PrefectureData

{

public readonly int id;

// 県庁所在地名

public readonly string name;

// 経度

public readonly double longitude;

// 緯度

public readonly double latitude;

// Unity上のオブジェクト

public GameObject ownObj;

public PrefectureData(List<string> csvLine)

{

id = int.Parse(csvLine[0]);

name = csvLine[1];

latitude = double.Parse(csvLine[2]);

longitude = double.Parse(csvLine[3]);

}

public class Salesman
{
    // 初期体力
    public float defaultStamina = 100;
    // 確率調整用のパラメータ
    public float rate = 1f;
    // 体力減少率
    public float decreaseRate = 0.98f;
    // この数値以下になった時、巡回を終了する
    public float finalStamina = 1.0e-7f;
    // 現在の体力
    public float stamina;
 
    public Salesman()
    {
        stamina = defaultStamina;
    }

    /// <summary>
    /// 距離が長くても選択するかどうか
    /// </summary>
    public bool Judge()
    {
        float rot = Random.Range(0, defaultStamina);
        return rot < stamina * rate;
    }

    /// <summary>
    /// 体力を減少する
    /// </summary>
    public void Travel() 
    {
        stamina *= decreaseRate;
    }

    /// <summary>
    /// 体力リセット
    /// </summary>
    public void Reset()
    {
        stamina = defaultStamina;
    }
}

public class Salesman

{

// 初期体力

public float defaultStamina = 100;

// 確率調整用のパラメータ

public float rate = 1f;

// 体力減少率

public float decreaseRate = 0.98f;

// この数値以下になった時、巡回を終了する

public float finalStamina = 1.0e-7f;

// 現在の体力

public float stamina;

public Salesman()

{

stamina = defaultStamina;

}

/// <summary>

/// 距離が長くても選択するかどうか

/// </summary>

public bool Judge()

{

float rot = Random.Range(0, defaultStamina);

return rot < stamina * rate;

}

/// <summary>

/// 体力を減少する

/// </summary>

public void Travel()

{

stamina *= decreaseRate;

}

/// <summary>

/// 体力リセット

/// </summary>

public void Reset()

{

stamina = defaultStamina;

}

    /// <summary>
    /// 最短経路に近い経路を求める
    /// </summary>
    /// <param name="prefectureList">県庁所在地データ</param>
    /// <returns>route:経路 distance:総距離</returns>
    private (List<PrefectureData> route, double distance) SolveTsp(List<PrefectureData> prefectureList)
    {
        _salesman.Reset();
        
        // ルート
        List<PrefectureData> optimalRoute = null;
        double optimalDistance = 0f;

        int loopCount = 0;

        while (_salesman.stamina > _salesman.finalStamina) {

            // 現在居る県
            var currentPref = prefectureList[Random.Range(0, prefectureList.Count)];

            // スタート県
            var startPref = currentPref;
            // 巡回予定の県
            var targetPrefs = prefectureList.ToList();
            targetPrefs.Remove(startPref);

            // 前回検索した県
            PrefectureData prevPref = null;
            // 前回の距離を保存
            double prevDistance = 0f;
            // 未判定の県
            var undecidedPrefs = targetPrefs.ToList();
            
            // 現在のルート
            List<PrefectureData> currentRoute = new List<PrefectureData>();
            currentRoute.Add(startPref);

            // 総移動距離
            double totalDistance = 0f;

            while (true) {
                loopCount++;
                var nextPref = undecidedPrefs[Random.Range(0, undecidedPrefs.Count)];

                // 次の地点の距離
                double nextDistance = GeoUtil.GeoDistance(nextPref.latitude, nextPref.longitude, currentPref.latitude,
                    currentPref.longitude, 10);

                // 判定対象から削除
                undecidedPrefs.Remove(nextPref);

                // 判定対象がない場合
                if (prevPref == null) {
                    if (undecidedPrefs.Count <= 0) {
                        // 巡回終了
                        currentRoute.Add(nextPref);
                        totalDistance += nextDistance;
                        currentRoute.Add(startPref);
                        totalDistance += GeoUtil.GeoDistance(nextPref.latitude, nextPref.longitude, startPref.latitude,
                            startPref.longitude, 10);
                        break;
                    }
                    prevPref = nextPref;
                    prevDistance = nextDistance;
                    continue;
                }

                // 二つの地点の距離判定
                if (nextDistance < prevDistance) {
                    // 前回判定したものよりも距離が短い
                    prevPref = nextPref;
                    prevDistance = nextDistance;
                } else if (_salesman.Judge()) {
                    // 距離が長くても交換する
                    prevPref = nextPref;
                    prevDistance = nextDistance;
                }

                // 判定対象がない場合は経路決定
                if (undecidedPrefs.Count <= 0) {
                    currentRoute.Add(prevPref);
                    totalDistance += prevDistance;
                    targetPrefs.Remove(prevPref);
                    undecidedPrefs = targetPrefs.ToList();
                    currentPref = prevPref;
                    prevPref = null;
                }
            }
            
            // 体力減少
            _salesman.Travel();

            if (optimalRoute == null) {
                // 最初の検索
                optimalRoute = currentRoute;
                optimalDistance = totalDistance;
            } else {
                // ２回目以降はトータル距離が短いものを選択
                if (totalDistance < optimalDistance) {
                    optimalRoute = currentRoute;
                    optimalDistance = totalDistance;
                }
            }
        }
        
        Debug.Log($"LoopCount:{loopCount}");
        
        return (optimalRoute, optimalDistance);
    }

100

101

102

103

104

105

106

107

108

109

/// <summary>

/// 最短経路に近い経路を求める

/// </summary>

/// <param name="prefectureList">県庁所在地データ</param>

/// <returns>route:経路 distance:総距離</returns>

private (List<PrefectureData> route, double distance) SolveTsp(List<PrefectureData> prefectureList)

{

_salesman.Reset();

// ルート

List<PrefectureData> optimalRoute = null;

double optimalDistance = 0f;

int loopCount = 0;

while (_salesman.stamina > _salesman.finalStamina) {

// 現在居る県

var currentPref = prefectureList[Random.Range(0, prefectureList.Count)];

// スタート県

var startPref = currentPref;

// 巡回予定の県

var targetPrefs = prefectureList.ToList();

targetPrefs.Remove(startPref);

// 前回検索した県

PrefectureData prevPref = null;

// 前回の距離を保存

double prevDistance = 0f;

// 未判定の県

var undecidedPrefs = targetPrefs.ToList();

// 現在のルート

List<PrefectureData> currentRoute = new List<PrefectureData>();

currentRoute.Add(startPref);

// 総移動距離

double totalDistance = 0f;

while (true) {

loopCount++;

var nextPref = undecidedPrefs[Random.Range(0, undecidedPrefs.Count)];

// 次の地点の距離

double nextDistance = GeoUtil.GeoDistance(nextPref.latitude, nextPref.longitude, currentPref.latitude,

currentPref.longitude, 10);

// 判定対象から削除

undecidedPrefs.Remove(nextPref);

// 判定対象がない場合

if (prevPref == null) {

if (undecidedPrefs.Count <= 0) {

// 巡回終了

currentRoute.Add(nextPref);

totalDistance += nextDistance;

currentRoute.Add(startPref);

totalDistance += GeoUtil.GeoDistance(nextPref.latitude, nextPref.longitude, startPref.latitude,

startPref.longitude, 10);

break;

}

prevPref = nextPref;

prevDistance = nextDistance;

continue;

}

// 二つの地点の距離判定

if (nextDistance < prevDistance) {

// 前回判定したものよりも距離が短い

prevPref = nextPref;

prevDistance = nextDistance;

} else if (_salesman.Judge()) {

// 距離が長くても交換する

prevPref = nextPref;

prevDistance = nextDistance;

}

// 判定対象がない場合は経路決定

if (undecidedPrefs.Count <= 0) {

currentRoute.Add(prevPref);

totalDistance += prevDistance;

targetPrefs.Remove(prevPref);

undecidedPrefs = targetPrefs.ToList();

currentPref = prevPref;

prevPref = null;

}

// 体力減少

_salesman.Travel();

if (optimalRoute == null) {

// 最初の検索

optimalRoute = currentRoute;

optimalDistance = totalDistance;

} else {

// ２回目以降はトータル距離が短いものを選択

if (totalDistance < optimalDistance) {

optimalRoute = currentRoute;

optimalDistance = totalDistance;

}

Debug.Log($"LoopCount:{loopCount}");

return (optimalRoute, optimalDistance);

}

月	火	水	木	金	土	日
« 10月
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30