目次
はじめに
こんにちは、いっちゃんです。入社した年の4月末に「&JO1」というゲームを開発するプロジェクトに配属されましたが、9月からは別の新規プロジェクトでサーバーサイドのソフトウェア開発に携わっています。
本記事では、2022年10月31日に開催された社内勉強会の内容をまとめます。10ANTZのエンジニアの間では不定期で勉強会が開催されており、業務と直接関係あるかどうかに関わらず幅広いテーマが取り上げられています。今回のテーマは、ファジィ理論とその応用例の紹介でした。具体的な内容は以下の通りでした。
- ソフトコンピューティングにおけるファジィ理論
- ファジィ集合に基づくファジィ理論のアプローチ
- 最近のファジィ理論の応用例
以下では、これらの内容について、私の理解をまとめていきます。
ソフトコンピューティングにおけるファジィ理論
ソフトコンピューティング
Wikipediaのソフトコンピューティングのページによれば、「ソフトコンピューティングの基本的な考え方は「不正確、不確実、および部分的な正しさを大目に見て利用することで、扱いやすさや頑強性や低コストを達成する」ことである」ということですが、私はこれを次のように理解しています。
- ソフトコンピューティングとは、複雑過ぎて現実的に解くことが困難な問題に対して,現実的な手段により(最適解でないかもしれないが)役に立つ解を求めようとする計算手法の総称を指している。
ソフトコンピューティングの例
以下にソフトコンピューティングの例を示します。
機械学習
機械学習では、複雑で構造が分からない現象について、その入力と出力からなるデータに基づいた予測を可能にします。ここでは、現象から得られたデータにフィットするようなニューラルネットワークを構築し、これにより、データを生じさせた元の現象を近似して、役に立つ予測を行うことができるようになります。
進化計算
進化計算では、最適解を求めることが現実的に不可能な最適化問題に対して、発見的な手法により実行可能な解を求めます。ここで、発見的な手法とは、得られる解の精度が保証されなくても、役に立つ解を得られるような手法で、例えば、遺伝的アルゴリズムや粒子群最適化といったものがあります。
ファジィ理論
ファジィ理論は、人間の主観に起因するあいまいさを含む問題を扱えるようにするための数学的な枠組みを与えます。ここでは、扱いたい対象があいまいさを含んでいたとしても、これをファジィ集合として表現することで、計算機で処理できるようになります。
ファジィ理論の位置付け
機械学習は、複雑な現象の入力と出力の関係を、データに基づいて統計的に求めます。進化計算は、複雑な最適化問題を、経験に基づく探索により、解を求めます。しかしここでは人間の主観に起因するあいまいさは扱えません。
これに対して、ファジィ理論は、人間の主観に起因するあいまいさを含む問題を扱うためのものと位置付けることができると思います。
ファジィ集合に基づくファジィ理論のアプローチ
「ファジィ」の意味合い
「ファジィ」とは、境界が明確でないようなあいまいな状態を意味する単語です。ファジィ理論が扱うあいまいさは、人間の主観に依存して集合の境界や命題の真偽が明確でないことにより生じるあいまいさです。例えば、「いっちゃんは背が高い」という主張には、高い身長とはどの程度の身長かというあいまいさがあり、このあいまいさは人間の主観に起因しています。
ファジィ理論のアプローチ
ファジィ理論を利用した多くのシステムでは、ファジィ集合とファジィ論理を使って推論(ファジィ推論)を行います。ファジィ集合は、あいまいな対象を数学的に表現するものです。ファジィ論理は、ファジィ集合に基づいてあいまいさを含む命題を扱うものです。社内勉強会では、基礎となるファジィ集合について次のような紹介がありました。
ファジィ集合
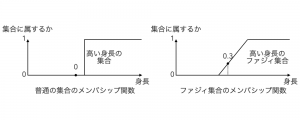
ファジィ理論では、通常の集合を「値がその集合に属するかどうか(属するなら1、属さないなら0)を返す関数」であるメンバシップ関数により境界が特徴づけられるものと捉え、これを拡張してファジィ集合を定義します。具体的には、ファジィ集合ではメンバシップ関数を、その集合に属するかどうかをその程度に応じて0から1までの範囲の実数として返すように拡張し、これにより集合の境界を特徴づけます。例えば、メンバシップ関数の返り値が0なら値が完全に属していないこと、0.5なら属しているかどうかが不明であること、1なら完全に属していることを表します。ファジィ理論を利用したシステムでは、設計者がメンバシップ関数を決定します。
例として、高い身長の集合のメンバシップ関数と高い身長のファジィ集合のメンバシップ関数を以下に示します。ファジィ集合では集合の境界がグラデーションとなるため、値をロバストに扱うことができます。
最近のファジィ理論の応用例
ファジィ理論により、人間の主観に起因するあいまいさを計算機で扱うことができるため、ヒューマンコンピュータインタラクションの分野で応用されることがあります。勉強会では、ファジィ理論を応用した最近の例として、以下のようなCADインターフェースの紹介がありました。
まとめ
社内勉強会で、ファジィ理論とその応用例が紹介されました。私の理解を端的にまとめると以下のようになります。
- ソフトコンピューティングにおいて、ファジィ理論は人間の主観に起因するあいまいさを含む問題を扱うためのものと位置付けることができる。
- ファジィ理論では、扱う対象があいまいさを持っていても、それをファジィ集合として表現することで、計算機で扱うことができるようになる。
- ファジィ理論は、ヒューマンコンピュータインタラクションの分野で応用されることがある。
参考文献
本記事をまとめる際に以下を参考にしました。
- https://www.ieice-hbkb.org/files/ad_base/view_pdf.html?p=/files/S3/S3gun_04hen_02.pdf
- https://www.ieice-hbkb.org/files/ad_base/view_pdf.html?p=/files/S3/S3gun_04hen_03.pdf
- https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%B8%E3%82%A3%E8%AB%96%E7%90%86
- https://ja.wikipedia.org/wiki/%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92
- https://ja.wikipedia.org/wiki/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%A9%E3%83%AB%E3%83%8D%E3%83%83%E3%83%88%E3%83%AF%E3%83%BC%E3%82%AF
- https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%B8%E3%82%A3%E9%9B%86%E5%90%88



