分析グループに所属しています。安部と申します。
分析する対象によって数字をどのように扱うのか(平均、中央値、標準偏差、etc…)は、データ分析においてとても重要なことだと思います。
今回は、そのような数字の扱い方について面白いパラドックスがあったので紹介したいと思います。
例として、ゲーム内で実施したイベントが成功だったのか失敗だったのか判断をするための分析を行っていたとします。
ここでは問題をシンプルにするために各イベントでユーザーがどの程度ポイントを獲得したのかを判断材料として考えたいと思います。
ユーザー一人一人のポイントを追っていては日が暮れてしまうので
情報を集約するため、一定のポイント層ごとに平均を算出しました。
| 獲得ポイント層 | イベントA(ポイント) | イベントB(ポイント) |
| 1000万ポイント以上 | 1700万 | 1760万 |
| 500万以上~1000万ポイント未満 | 700万 | 800万 |
| 100万以上~500万ポイント未満 | 260万 | 400万 |
| 100万ポイント未満 | 50万 | 59万 |
集計した結果が上の表のようになったとします。
この結果を見てどのように感じるでしょうか。
これだけを見ると「イベントBはイベントAよりも、どの層でも平均ポイントが上がっている。つまりイベントAに比べてイベントBは成功だ」
と、言えるかもしれません。
それでは次に、ポイント層で分けずに全体で平均を出してみます。
| イベントA(ポイント) | イベントB(ポイント) |
| 678万 | 542万 |
全体平均でみるとイベントBの方がイベントAよりも低くなってしまいました。
層ごとの平均ではイベントBが上なのに、全体平均ではイベントAの方が上です。
これはどちらのイベントが成功と言えるのでしょうか。
数字を見る際にこのパラドックスは心に留めておくべき問題だと思いましたので、ブログにしてみました。
それではなぜ上のような現象が起こっているのかを以下の図で説明します。
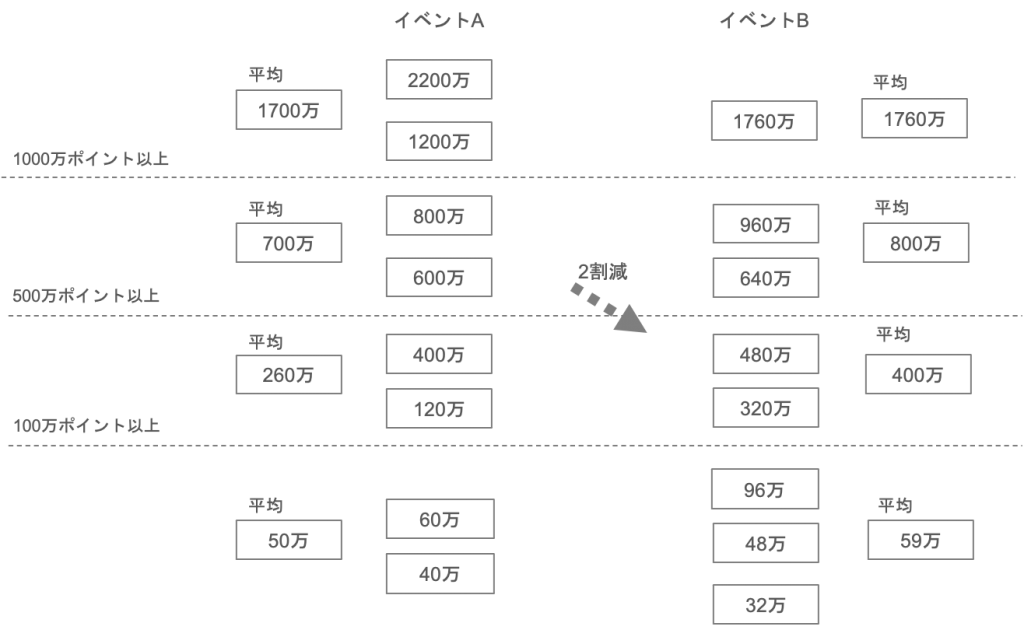
上の図のように、全体としてはポイントが2割減っています。
そのため、「1000万ポイント以上」の層にぎりぎりいた1200万ポイントのユーザーが「500万ポイント以上」の層に移動し、
「500万ポイント以上」の層にいた600万ポイントのユーザーがその下の層へ、、
というようにそれぞれ層の移動が起こっています。
その結果、各層の平均値を下げていた原因である比較的ポイントが低かったユーザーがいなくなったので、
各層の平均値自体は上昇しています。
このように、「集団全体の性質と、集団を分けたときの性質が異なる」現象は
シンプソンのパラドックスと呼ばれるものです。
これが仮に実業務の中のデータ分析で、各層の平均だけを見て判断してしまった場合、
間違った分析結果を共有してしまう危険性があります。
平均値は、多くの情報を集約するのに便利で使いやすいですが、
使い方を誤ると真逆の結果を与えてしまうため、意味をよく理解して使っていきたいですね。
数字を扱う業務に携わるものとして、数字に騙されないよう注意していきたいです。
参考文献
神永正博(2018/10/01)直感を裏切る数学 「思い込み」にだまされない数学的思考法 講談社



