目次
はじめに
統計学は、推測統計学、記述統計学、ベイズ統計学の大きく3つに分けることができます。
記述統計学 :収集したデータの統計量を計算し、データの傾向や性質を知るものです
推測統計学 :母集団から採取したデータの特徴から母集団の特性を推測します
ベイズ統計学 :ベイズの定理を用いた統計学です
また、推測統計学は、統計的推定、統計的仮説検定の2つに分けることができます。
統計的推定 :母集団の標本データから母集団の特性値を統計学的に推定します
統計的仮説検定:母集団から採取したデータに対する統計量が正しいかを統計学的に検証します
今回は推測統計学の統計的仮説検定で用いる検定法の1つである「カイ2乗検定」を学習しようと思います。
※検定法には、以下のような種類があります。
・t分布による検定
・F分布による検定
・カイ2乗分布による検定
・正規分布による検定
統計的仮説検定の手順
① 仮説を設定します
仮説を立てます。仮説は、導きたい結論とは反対の仮説を設定します。
帰無仮説 :設定する仮説(棄却されることを期待して立てられる仮説)
対立仮説 :導き出したい結論(帰無仮説が棄却されたときに採用される仮説)
② 有意水準を決定します
「5%(0.05)」に設定します。
有意水準とは、設定した仮説が間違っていると判断する(仮説を棄却する)確率のことで、5%や1%が多く使われます。有意水準を5%に設定した場合、5%以下の確率で生じる現象は、非常にまれなことであるとします。
③ 検証します
データから仮説の確率を算出して、検証します。
④ 結論を導きます
検証した結果、設定した仮説が有意水準で指定した棄却域に入らない場合は、帰無仮説が正しいとします。
逆に有意水準で指定した棄却域に入る場合は、対立仮説が正しいとします。
※仮説検定には、2種類の誤りが生じ得ます。
1つは、帰無仮説が正しい時に帰無仮説を棄却する誤り、もう1つは、対立仮説が正しい時に帰無仮説を棄却しない誤りです。
帰無仮説が正しい時に帰無仮説を棄却する誤りを第1種過誤、対立仮説が正しい時に帰無仮説を棄却しない誤りを第2種過誤といいます。
| 判断 | 帰無仮説が正しい | 対立仮説が正しい |
| 帰無仮説を棄却 | 第1種過誤 | 正しい |
| 帰無仮説を受容 | 正しい | 第2種過誤 |
Rを使って独立性の検定(カイ2乗検定)を実施
統計解析ソフトRを使って、カイ2乗検定を実施してみます。
※Rのインストール方法については、ここでは省略させていただきます。
検定内容
ゲームのジャンルでRPGを遊んだことがある100人に「遊ぶ頻度」、「レベル上げが好きかどうか」についてアンケートをとった結果、下記のような回答結果になった場合、「遊ぶ頻度」と「レベル上げが好きかどうか」に関連性は有ると言えるかを有意水準5%で検定します。
※回答は、実際のデータではありません。学習用に作成したデータです。
| (1) レベル上げが好き | (2) レベル上げが嫌い | 合計 | |
| (A) よくRPGを遊ぶ | 30 | 20 | 50 |
| (B) RPGはあまり遊ばない | 18 | 32 | 50 |
| 合計 | 48 | 52 | 100 |
帰無仮説と対立仮説
帰無仮説:「RPGを遊ぶ頻度」と「レベル上げが好きかどうか」は独立である(関連性はない)
対立仮説:「RPGを遊ぶ頻度」と「レベル上げが好きかどうか」は独立ではない(関連性がある)
ソースコード

(補足)
24行目:検定統計量 =(実際の観測値ー期待値)の2乗 / 期待値
※期待値:ある試行を繰り返した時に得られる実現値の平均
30行目:qchisq関数の第1引数は有意水準、第2引数は自由度を指定します。
※自由度:クロス集計表がm×nの場合、自由度は、(m-1)×(n-1)
34行目:chisq関数を使用してカイ2乗の実現値の算出も可能です。
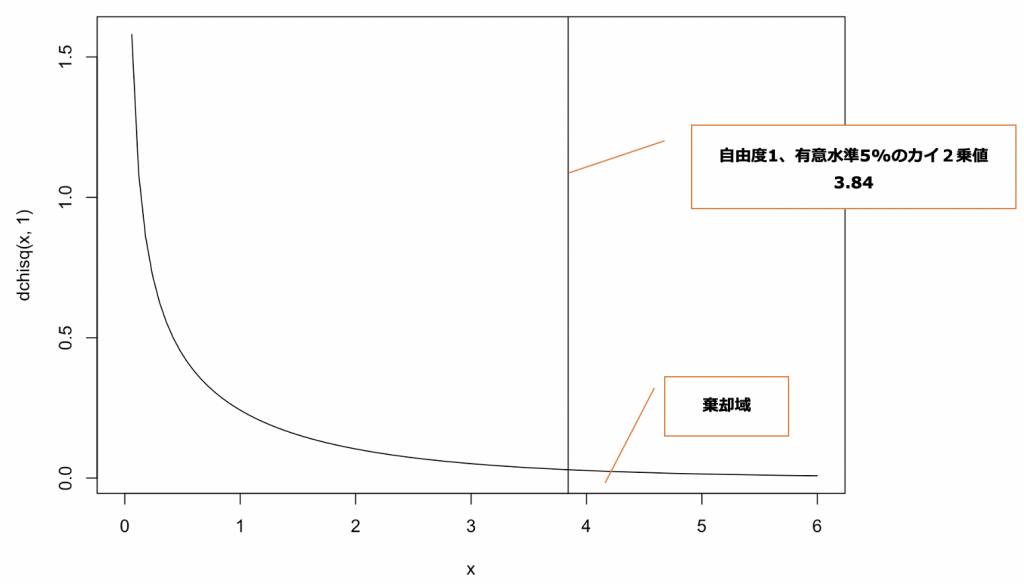
自由度1のカイ2乗分布

自由度1、有意水準5%のカイ2乗分布です。カイ2乗値「3.84」の左側の面積が95%、右側の面積が5%になります。
検定統計量の実現値と「3.84」を比較して結論を出します。
検定統計量の実現値が「3.84」よりも大きい場合は、「5%よりも小さい確率で起こる(稀にしか起こらない)」ということになります。
※chisq関数の結果

結果
検定統計量の実現値「5.77」は、有位水準5%のカイ2乗値「3.84」より大きいので、帰無仮説を棄却し、対立仮説を採択します。
したがって、「RPGを遊ぶ頻度」と「レベル上げが好きかどうか」には、関連性があるという結論になります。
まとめ
今回は統計的仮説検定で用いる検定法の1つである「カイ2乗検定」について統計解析ソフトRを使用して学習しました。
当たり前ですが、データを分析する場合、主観に頼らず統計的に判断することが大切です。
統計解析ソフトRは、大変便利なデータマイニングツールなので、これからも利用していきたいと思います。
参考文献
金城 俊哉 著「R統計解析パーフェクトマスター」, 秀和システム



